1.1 The Core Synchronous Language
1.1.1 Point-wise Operations
Zélus is a first-order functional language. As in Lustre, every ground type or scalar value is imported from a host language (OCaml) and implicitly lifted to signals. A signal is a sequence or stream of values ordered in time: a value at an instant can only be produced after the values at all previous instants have been produced. This property models causality. In particular,
- int stands for the type of streams of integers,
- 1 stands for the constant stream of 1s,
- + stands for the pointwise addition operator over two input streams. It can be seen as an adder circuit just as && can be seen as an “and” gate.
Program executions can be represented as timelines showing the sequences of values taken by streams. The example below shows five streams, one per line. The first line shows a stream c, which has the value T (true) at the first instant, F (false) at the second one, and T at the third. The ‘⋯’ indicates that the stream has infinitely more values that are not shown. The next two lines define x and y. The fourth line defines a stream obtained by the pointwise addition of x and y. The expression in the fifth line takes the current value of either x or y according to the current value of c.
| c | true | false | true | ⋯ |
| x | x0 | x1 | x2 | ⋯ |
| y | y0 | y1 | y2 | ⋯ |
| x+y | x0 + y0 | x1 + y1 | x2 + y2 | ⋯ |
| if c then x else y | x0 | y1 | x2 | ⋯ |
1.1.2 Delays
The delay operator is denoted fby. The expression x fby y, which is read as “x followed by y” takes the first value of x at the first instant and the previous value of y at all instants thereafter. In other words, it delays y by one instant, and is initialized by x. This operator originated in the language Lucid [1].
| x | x0 | x1 | x2 | ⋯ |
| y | y0 | y1 | y2 | ⋯ |
| x fby y | x0 | y0 | y1 | ⋯ |
As it is often useful to separate a delay from its initialization, there is an operator pre x that delays its argument x and has an unspecified value (denoted here by nil) at the first instant. The complementary initialization operator x -> y takes the first value of x at the first instant, and the current value of y thereafter. The expression x -> (pre y) is equivalent to x fby y.
| x | x0 | x1 | x2 | ⋯ |
| y | y0 | y1 | y2 | ⋯ |
| pre x | nil | x0 | x1 | ⋯ |
| x -> y | x0 | y1 | y2 | ⋯ |
The compiler performs an initialization check to ensure that the behavior of a program never depends on the value nil. See section 1.1.9 for details.
Note:
A common error is to try to use the initialization operator to define the first two values of a stream. This does not work, since x -> y -> z = x -> z. One should instead write either x fby y fby z or x -> pre (y -> pre z). For example, the stream which starts with a value 1, followed by a 2, and then 3 forever is written 1 fby 2 fby 3 or 1 -> pre(2 -> pre(3)) or 1 -> pre(2 -> 3).
1.1.3 Global Declarations
A program is a sequence of declarations of global values. The keyword let defines non recursive global values which may be either constants or functions. For example:
let dt = 0.001
let g = 9.81
These declarations define two constant streams dt and g. Given the option -i, the compiler displays the types inferred for each declaration:
aneto.local: zeluc.byte -i tutorial.zls
Only constant values can be defined globally. The declaration
let first = true -> false
is rejected with the message:
aneto.local: zeluc.byte -i tutorial.zls
The right-hand side of a global let declaration may not contain delay operations. Definitions containing delays require the introduction of state. They may only be made within the node definition described in section 1.1.5.
1.1.4 Combinatorial Functions
Functions whose output at an instant depends only on inputs at the same instant are termed combinatorial. They are stateless and may thus be used in both discrete and continuous time. Any expression without delays, initialization operators, or automata is necessarily combinatorial.
As for any globally defined value, a combinatorial function is defined using the let keyword. Consider, for example, a function computing the instantaneous average of two inputs:
let average (x,y) = (x + y) / 2
The type signature inferred by the compiler, int * int -A-> int, indicates that it takes two integer streams and returns an integer stream. The arrow -A-> tagged with an A indicates that this function is combinatorial. The A stands for “any”—the function average can be used anywhere in the code. We will describe other possibilities soon.
Function definitions may contain local declarations, introduced using either where or let notations. For example, the average function can be written in two (equivalent) ways:
let average (x,y) = o where o = (x + y) / 2
and
let average (x,y) = let o = (x + y) / 2 in o
The full adder is a classic example of a combinatorial program. It takes three input bits, a, b, and a carry bit c, and returns outputs for the sum s and carry-out co.
let xor (a, b) = (a & not(b)) or (not a & b)
let full_add (a, b, c) = (s, co) where
s = xor (xor (a, b), c)
and co = (a & b) or (b & c) or (a & c)
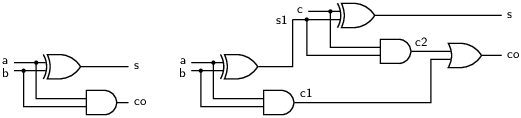
Alternatively, a full adder can be described more efficiently as a composition of two half adders. A graphical depiction is given in figure 1.1. The corresponding program text is:
let half_add(a,b) = (s, co) where
s = xor (a, b)
and co = a & b
let full_add2(a, b, c) = (s, co) where
rec (s1, c1) = half_add(a, b)
and (s, c2) = half_add(c, s1)
and co = c1 or c2
The rec keyword specifies that the block of equations following the where is defined by mutual recursion. Without it, the s1 in the equation for s and c2 would have to exist in the list of inputs or the global environment, and similarly for c1 and c2 in the equation for co.
Alternative notation:
For combinatorial function definitions, the keyword let can be replaced by fun.
fun half_add (a,b) = (s, co) where
rec s = xor (a, b)
and co = a & b
1.1.5 Stateful Functions
A function is stateful or sequential if its output at an instant n depends on the inputs at previous instants k (k ≤ n), that is, on the history of inputs. Such functions may produce a varying output signal even when their inputs are constant.
Stateful functions must be declared with the node keyword. For example, this function computes the sequence of integers starting at an initial value given by the parameter m:
let node from m = nat where
rec nat = m -> pre nat + 1
The type signature int -D-> int indicates that from is a sequential function that maps one integer stream to another. The D indicates that this function is stateful, it stands for “discrete”. The function’s output may depend on the past values of its input.
Applying this function to the constant stream 0 yields the execution:
| m | 0 | 0 | 0 | 0 | 0 | 0 | ⋯ |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | ⋯ |
| pre nat | nil | 0 | 1 | 2 | 3 | 4 | ⋯ |
| pre nat + 1 | nil | 1 | 2 | 3 | 4 | 5 | ⋯ |
| m -> pre nat + 1 | 0 | 1 | 2 | 3 | 4 | 5 | ⋯ |
| from m | 0 | 1 | 2 | 3 | 4 | 5 | ⋯ |
The fact that a function is combinatorial is verified during compilation. Thus, omitting the node keyword,
let from n = nat where rec nat = n -> pre nat + 1
leads to an error message:
aneto.local: zeluc.byte -i tutorial.zls
While a node (arrow type -D->) cannot be called within a combinatorial function, it is possible to call a combinatorial function (arrow type -A->) within in a node. For example, the addition operator in the from function has the type signature int * int -A-> int.
We now present a few more examples of stateful functions.
The edge front detector is defined as a global function from boolean streams to boolean streams:
let node edge c = c & not (false fby c)
| c | false | false | true | true | false | true | ⋯ |
| false | false | false | false | false | false | false | ⋯ |
| false fby c | false | false | false | true | true | false | ⋯ |
| not (false fby c) | true | true | true | false | false | true | ⋯ |
| edge c | false | false | true | false | false | true | ⋯ |
A forward Euler integrator can be defined by:
let dt = 0.01
let node integr (x0, x') = x where
rec x = x0 -> pre (x +. x' *. dt)
These declarations give a global function integr that returns a stream x defined recursively so that, for all n ∈ IN, x(n) = x0 + ∑i=0n−1 x′(i)· dt. The operators ‘+.’ and ‘*.’ are, respectively, addition and multiplication over floating-point numbers. Stateful functions are composed just like any other functions, as, for example, in:
let node double_integr (x0, x0', x'') = x where
rec x = integr (x0, x')
and x' = integr (x0', x'')
Alternative notation:
The keyword let can be omitted, for example,
let dt = 0.01
node integr (x0, x') = x where
rec x = x0 -> pre (x +. x' *. dt)
1.1.6 Local and Mutually Recursive Definitions
Variables may be defined locally with let/in or let rec/in whether the defining expression is stateful or not. The following program computes the Euclidean distance between two points:
let distance ((x0,y0), (x1,y1)) =
let d0 = x1 -. x0 in
let d1 = y1 -. x1 in
sqrt (d0 *. d0 +. d1 *. d1)
Since d0 and d1 denote infinite streams, the computations of x1 -. x0 and y1 -. x1 occur in parallel, at least conceptually. In Zélus, however, the consecutive nesting of let/ins introduces a sequential ordering on the computations at an instant. In this example, this means that the current value of d0 is always computed before the current value of d1. Being able to impose such an ordering is useful when functions with side-effects are imported from the host language. Write simply let rec d0 = ... and d1 = ... if no particular ordering is needed.
Streams may be defined through sets of mutually recursive equations. The function that computes the minimum and maximum of an input stream x can be written in at least three equivalent ways. As two mutually recursive equations after a where:
let node min_max x = (min, max) where
rec min = x -> if x < pre min then x else pre min
and max = x -> if x > pre max then x else pre max
as a stream of tuples defined by two local, mutually recursive equations:
let node min_max x =
let rec min = x -> if x < pre min then x else pre min
and max = x -> if x > pre max then x else pre max in
(min, max)
or as a stream of tuples defined by a single recursive equation:
let node min_max x = (min, max) where
rec (min, max) = (x, x) -> if x < pre min then (x, pre max)
else if x > pre max then (pre min, x)
else (pre min, pre max)
Discrete approximations to the sine and cosine functions can be defined by:
let node sin_cos theta = (sin, cos) where
rec sin = integr(0.0, theta *. cos)
and cos = integr(1.0, -. theta *. sin)
1.1.7 Shared Memory and Initialization
In addition to the delay operator pre, Zélus provides another construction for referring to the previous value of a stream: last o, where o is a variable defined by an equation. For example:
let node counter i = o where
rec init o = i
and o = last o + 1
The equation init o = i defines the initial value of the memory last o. This memory is initialized with the first value of i and thereafter contains the previous value of o. The above program is thus equivalent to the following one:1
let node counter i = o where
rec last_o = i -> pre o
and o = last_o + 1
The reason for introducing memories will become clear when control structures are introduced in section 1.2.2. Syntactically, last is not an operator: last o denotes a shared memory and the argument of last, here o, must be a variable name. Thus this program is rejected:
let node f () = o where
rec o = 0 -> last (o + 1)
Rather than define the current value of a signal in terms of its previous one, the next value can also be defined in terms of the current one. The same counter program can be written:
let node counter i = o where
rec init o = i
and next o = o + 1
or equivalently:
let node counter i = o where
rec next o = o + 1 init i
In both definitions, o is initialized with the first value of i and then the value of o at instant n+1 is the value of o + 1 at instant n (for all n ∈ IN).
Neither the form defining the current value from the previous one, nor the form defining the next value from the current one is intrinsically superior; it depends on the situation. Either form can be transformed into the other. We will see in chapter 2 that restrictions apply to both the next and last constructions when combining discrete- and continuous-time dynamics.
Remark: The compiler rewrites last, ->, fby, pre,
init and next into a minimal subset.
1.1.8 Causality Check
Instantaneous cycles between recursively defined values—causality loops—are forbidden so that the compiler can produce statically-scheduled sequential code. For example, the program:
let node from m = nat where
rec nat = m -> nat + 1
is rejected with the message:
This program cannot be computed since nat depends instantaneously on itself. The compiler statically rejects function definitions that cannot be scheduled sequentially, that is, when the value of a stream at an instant n may be required in the calculation of that very value at the same instant, whether directly or through a sequence of intermediate calculations. In practice, we impose that all such stream interdependencies be broken by a delay (pre or fby). The purpose of causality analysis to to reject all other loops.
Note that delays can be hidden internally in the body of a function as is the case, for instance, in the languages Lustre and Signal. For example, consider the initial value problem:
|
We can approximate this value by using the explicit Euler integrator defined previously and defining a signal t by a recursive equation.
(* [t0] is the initial temperature; [g0] and [g1] two constants *)
let node heater(t0, g0, g1) = t where
rec t = integr(t0, g0 -. g1 *. t)
This feedback loop is accepted because integr(t0, g0 -. g1 *. temp) does not depend instantaneously on its input.
It is also possible to force the compiler to consider a function as strict with the atomic keyword. For example, the following program is rejected by the causality analysis.
let atomic node f x = 0 -> pre (x + 1)
let node wrong () =
let rec o = f o in o
Even though the output of f does not depend instantaneously on its input x, the keyword atomic adds instantaneous dependencies between the output and all inputs. For atomic functions, the compiler produces a single step function.2
1.1.9 Initialization Check
The compiler checks that every delay operator is initialized. For example,
let node from m = nat where
rec nat = pre nat + 1
The analysis [10] is a one-bit analysis where expressions are considered to be either always defined or always defined except at the very first instant. In practice, it rejects expressions like pre (pre e), that is, uninitialized expressions cannot be passed as arguments to delays; they must first be initialized using the -> operator.