1.2 Data types and Pattern Matching
1.2.1 Type Definitions
Product types, record types, and enumerated types are defined in a syntax close to that of OCaml. Constructors with arguments are not supported in the current release. They can nevertheless be defined together with the functions that manipulate them in an OCaml module which is then imported into Zélus; see section 4.12.
Records are defined as in Ocaml and accessed with the dot notation. For example, the following defines a type circle, representing a circle as a record containing a center, given by its coordinates, and a radius.
type circle = { center: float ∗ float; radius: float }
let center c = c.center
let radius c = c.radius
1.2.2 Pattern Matching
Pattern matching over streams uses a match/with construction like that of OCaml.
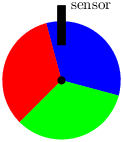
For example, consider a colored wheel rotating on an axis for which we want to compute the direction of rotation. As shown in figure 1.2, the wheel has three sections with colors, ordered clockwise, blue (Blue), green (Green), and red (Red) . A sensor mounted on the frame detects the changing colors as the wheel turns.
We must calculate whether the wheel is moving clockwise (Clockwise), that is, the sensor reports the sequence Red, Green, Blue, Red…, anticlockwise (Anticlockwise), whether it is not moving (Immobile), or whether the direction cannot be determined (Undetermined). We program the controller by first introducing two sum types:
type color = Blue | Red | Green
type dir = Clockwise | Anticlockwise | Undetermined | Immobile
The function direction then compares three successive values of the input stream i.
let node direction i = d where
rec pi = i fby i
and ppi = i fby pi
and match ppi, pi, i with
| (Red, Red, Red) | (Blue, Blue, Blue) | (Green, Green, Green) ->
do d = Immobile done
| (_, Blue, Red) | (_, Green, Blue) | (_, Red, Green) ->
do d = Clockwise done
| (_, Red, Blue) | (_, Green, Red) | (_, Blue, Green) ->
do d = Anticlockwise done
| _ -> do d = Undetermined done
end
Each handler in a pattern-matching construct contains a set of equations defining shared variables; here the variable d. At each instant, the match/with statement in the example selects the first pattern (from the top) that matches the actual value of the triple ppi, pi, i and executes the corresponding branch. Only one branch is executed in any single reaction.
Combining such control structures with delay operators can give rise to subtle behaviors. Consider, for instance, the following program with two modes: in the Up mode, the variable o increases by 1 at each reaction and, in the mode Down, it decreases by 1.
type modes = Up | Down
let node two (m, i) = o where
rec init o = i
and match m with
| Up -> do o = last o + 1 done
| Down -> do o = last o - 1 done
end
The equation init o = i defines a shared memory last o which is initialized with the first value of i. The variable o is called a shared variable because its definition is spread over several equations: when m equals Up, o equals last o + 1; when m equals Down, o equals last o - 1. Communication between the two modes occurs through the shared memory last o which contains the value that o had the last time that it was defined (that is, at the most recent previous instant of definition). An example execution diagram is given below.
| i | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ⋯ |
| m | Up | Up | Up | Down | Up | Down | Down | ⋯ |
| last o + 1 | 1 | 2 | 3 | 3 | ⋯ | |||
| last o - 1 | 2 | 2 | 1 | ⋯ | ||||
| o | 1 | 2 | 3 | 2 | 3 | 2 | 1 | ⋯ |
| last o | 0 | 1 | 2 | 3 | 2 | 3 | 2 | ⋯ |
An equivalent way to express the same behaviour is:
let node two (m, i) = o where
rec last_o = i -> pre o
and match m with
| Up -> do o = last_o + 1 done
| Down -> do o = last_o - 1 done
end
This version makes it clear how last o stands for the previously defined value of o.
The next section explains why using pre in this example would have given quite different results.
1.2.3 Pre versus Last
While last o may seem like just an alternative to pre o for referring to the previous value of a stream, there is a fundamental difference between the two based on their respective instants of observation.
- In Zélus, as in other block-diagram formalisms like Simulink and SCADE, pre e is a unit delay through a local memory—it denotes the value that its argument had the last time it was observed. If pre e is used in a block structure which is executed from time to time, for example, when some condition c is true, the argument e is only computed when c is true: pre e is the value of e the last time c was true.
- On the other hand, last o denotes the previous value of the variable o relative to the sequence of instants where the variable o (it must be a variable and not an expression) is defined. It is useful for communicating values between modes which is why it is called a shared memory.
We augment the previous example with extra equations to illustrate the difference between the two delay constructs. The two new streams c1 and c2 return respectively the number of instants in which each mode is active.
let node two (m, i) = (o, c1, c2) where
rec init o = i
and init c1 = 0
and init c2 = 0
and match m with
| Up -> do o = last o + 1
and c1 = 1 -> pre c1 + 1
done
| Down -> do o = last o - 1
and c2 = 1 -> pre c2 + 1
done
end
The equation c1 = 1 -> pre c1 + 1 is only active in the Up mode, and the equation c2 = 1 -> pre c2 + 1 is only active in the Down mode. The execution diagram is given below.
| i | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ⋯ |
| m | Up | Up | Up | Down | Up | Down | Down | ⋯ |
| last o + 1 | 1 | 2 | 3 | 3 | ⋯ | |||
| 1 -> pre c1 + 1 | 1 | 2 | 3 | 4 | ⋯ | |||
| last o - 1 | 2 | 2 | 1 | ⋯ | ||||
| 1 -> pre c2 + 1 | 1 | 2 | 3 | ⋯ | ||||
| o | 1 | 2 | 3 | 2 | 3 | 2 | 1 | ⋯ |
| last o | 0 | 1 | 2 | 3 | 2 | 3 | 2 | ⋯ |
| c1 | 1 | 2 | 3 | 3 | 4 | 4 | 4 | ⋯ |
| c2 | 0 | 0 | 0 | 1 | 1 | 2 | 3 | ⋯ |
Pattern matching composes complementary sub-streams. For instance, the match/with in the previous example has two branches, and each defines its own clock, one for the instants when m = Up and the other for the instants when m = Down.
1.2.4 Local Definitions
It is possible to define variables which are local to a branch. For example:
let node two (m, i) = o where
match m with
| Up -> let rec c = 0 -> pre c + 1 in
do o = c done
| Down -> do o = 0 done
end
or equivalently:
let node two (m, i) = o where
match m with
| Up -> local c in
do c = 0 -> pre c + 1
and o = c done
| Down -> do o = 0 done
end
Here, c is declared local to the first handler of the match/with statement. The compiler verifies that a definition for c is given. Several variables can be declared local by writing local c1,..., cn in ....
1.2.5 Implicit Completion of Shared Variables
The branches of a pattern-matching construct need not contain definitions for all shared variables. Branches without a definition for a shared variable o are implicitly completed with an equation o = last o.
The compiler rejects programs where it is unable to ensure that last o has an initial value. The following program, for instance, is rejected.
let node two (m, i) = o where
rec match m with
| Up -> do o = last o + 1 done
| Down -> do o = last o - 1 done
end